by

Samuel H. Williamson
President of MeasuringWorth
and
Professor of Economics, Emeritus
Miami University.^*

with

Louis P. Cain
Professor of Economics, Emeritus
Loyola University Chicago
and
Adjunct Professor of Economics
Northwestern University

“The real price of every thing, what every thing really costs to the man who wants to acquire it, is the toil and trouble of acquiring it. What everything is really worth to the man who has acquired it, and who wants to dispose of it or exchange it for something else, is the toil and trouble which it can save to himself, and which it can impose upon other people…. But though labour be the real measure of the exchangeable value of all commodities, it is not that by which their value is commonly estimated…. Every commodity, besides, is more frequently exchanged for, and thereby compared with, other commodities than with labour.

—Adam Smith, The Wealth of Nations, 1776.

 

Cecil Graham: What is a cynic?

Lord Darlington: A man who knows the price of everything, and the value of nothing.

Cecil Graham: And a sentimentalist, my dear Darlington, is a man who sees an absurd value in everything and doesn’t know the market price of any single thing.”

—Oscar Wilde, Lady Windermere’s Fan, 1892.

 

As these quotations show, both economists and non-economists have long commented on the nature of “worth” and “value.” Economists are often asked, “What is something worth?” Since that is not a very precise question, there is no precise answer. The usual answer uses the language of “opportunity cost;” the worth of something is “the cost of the most valuable forgone alternative.” The worth of something is relative; it can only be measured in terms of the value of something else. When the comparison involves time, the common practice is to inflate or deflate the number known at one point in time to the dollars of another point in time using a spliced price index such as the consumer price index (CPI). Yet, in most cases, the question “what is the current dollar price of a number from the past” is not a perfect substitute for the question “what is the relative value of a number from the past.” The greater the time difference between past and present, the greater the likelihood that the CPI will not reflect the item in the same manner at both times.

A second problem is that the “forgone alternative” is specific to the questioner; it differs for each individual. Thus, we usually use price to measure worth and let everyone “compute” the most valuable alternative that this amount of money would buy for him or her. There are many shortcomings to this approach, particularly when we attempt to make comparisons over different places or times – or between people with different backgrounds or resource endowments. Fortunately, there are alternatives to these answers. One is suggested in the Adam Smith quotation: we can measure the worth of something as the number of hours of labor (by the average worker) it takes to earn the amount of money that the item costs. This helps to alleviate some of the comparison problems, as “labor value" can be used with different currencies, different time periods, and different places. However, this approach has its problems and is only one of many alternatives.

To address these problems as consistently as possible, four comparators help explain that the answer to “how much is something worth” depends on the context of the question. (All four can be found on MeasuringWorth.com.) Measuring the worth of a loaf of bread differs substantially from measuring the worth of the Interstate Highway System.

It is unfortunate that modern conventional wisdom presents the problem of the measurement of “worth” over time as solved. It is not! Specifically, in the measurement of “worth,” almost all empirical applications identify “real price” or “real worth” with “deflation” by the consumer price index (CPI).^[1] While it is important to remove the inflationary component in intertemporal comparisons of worth, we maintain that “real price”—in practice, deflation by the CPI—often does not provide the comparison that one wants. The reason is that the result has been corrected only for the change in relative price between the item in question and a (conceptually) fixed or even varying bundle of consumer goods and services. While economists are trained to think in terms of relative prices, most non-economists do not. This is an issue where the average person would find “affordability” to be more understandable, and there is a lesson here for the economist.

This difference is illustrated by the changes in the price of gasoline. These days the “real price” of gasoline has been fluctuating around what it was in 1983 ($2.89 in 2017 dollars.). Economists might then say the burden was the same as it was a quarter century ago. Those who focus on affordability, however, would note the fact that real incomes have increased by about 75 percent during this period—in many contexts a fact more pertinent than the movement of the CPI.

A second example concerns the average salary of accountants. In 1931, the average accountant earned $2,250 in 1931 dollars. If you use the CPI to inflate that figure to 2017 dollars, you get a “real” wage of $36,200. Given the median wage of accountants in 2017 was $68,150, use of the CPI alone results in a significant underestimate in the absence of additional information. A different conclusion would be reached if we compare this to the “average household expenditure” (AHE) as measured by the BLS Consumer Expenditure Survey; $2,250 was 1.43 times the AHE for 1931. If one multiplies 1.43 times the AHE for 2017, the relative value of an accountant’s salary is $85,000. $2,250 in 1931 was 50% more than a full time, 60 hour a week production worker would have earned. If the ratio of unskilled wages in 2017 to 1931 is used, the relative value of an accountant’s salary is over $109,000. Similarly, using real GDP per capita yields $215,000 and just GDP leads to a relative salary of over $565,000. Given the wide range of these values, a case can be made for reporting more than one comparator.

The question of something’s relative “worth” is more complex than it seems, and we show that an unambiguous answer is impossible absent a specific context. Indeed, our empirical computations exhibit how different definitions of worth can give answers that differ by up to 2,000 times for a comparison between 1800 and today, depending on the “deflator” selected. The purpose of this paper is to develop a process to be used when relative “worth” is computed and to provide guidance for selection of the best definition, or often combination of definitions, of worth.

The paper begins with a process to create different definitions of worth for a single time period (or point in time). Empirical case studies are applied statically to the year 1931, with subjects ranging from the famous (salary of Babe Ruth, unpaid taxes of Al Capone, cost of Empire State Building) to the mundane (wage of an accountant), and from the large (U.S. defense budget) to the small (price of a loaf of bread). We show that the worth of subjects that existed in 1931 (or any other year) can be readily measured in terms of that year itself. The CPI is irrelevant.

Then the methodology is extended to intertemporal comparisons, with comparative-static computations of worth. The subjects from 1931 are assigned worth in terms of the year 2017, but any other year could be chosen. The CPI might be useful, but it is unlikely to provide the answer to what the questioner is asking.

This paper discusses how to compute the relative worth of an item and demonstrates that any item with an associated monetary amount can have its worth measured in many ways -- both at a moment in time and over time. The different definitions of relative worth presented show how important context is. The paper shows that statements of worth are meaningful only when the contexts are specified and that the almost uniform use of the CPI (particularly by itself) to measure worth over time is often misleading. Although there may be an implicit or explicit assumption that all these definitions will tell about the same story as we talk about the past, that by using one we are implying the others, this paper shows how wrong that is.

 

What Is Something Worth at a Point in Time?

In considering worth at a single point in time (or time period) rather than comparing it to another point, the conventional technique of inflating or deflating by an annual price index, such as the often-employed CPI, is not applicable. In principle, there can be thousands of ways to measure worth; most of them are independent of time. Every daily transaction involves an explicit or implicit computation of relative worth. Each transaction can be viewed from more than one perspective; so one measure may well not be sufficient.

When one purchases a $20 lunch, there are thousands of other items that this $20 could be spent on – a simple shirt, going to a movie (with popcorn), putting it in the collection plate at a church, and on and on. We all carry a conscious and subconscious list in our head of the opportunity cost of that lunch. But even if we are not buying a lunch, we can think about how there are lunches for $200 at some places and $4.50 at others. They may both have chicken in them, but we understand why they have different prices.

Each person’s list of what they would compare to that $20 lunch is different, and it is a list that changes over time and place. For the average person in an expensive neighborhood in New York, it would be very different than a person in a small town in Wyoming. It also might change for everyone if there is inflation.^[2]

This essay presents a general framework that defines nine broad-based terms or definitions that can be easily recognized and used to measure the relative worth of an item. First, when talking about the (relative) worth of an item, it should be categorized as a commodity, a project, or an observation of compensation or wealth. Then (and only then) should it be measured relative to well-defined indexes of economic activity that put the item in perspective. These indexes are referred to as “measures.”

 

The Categories of Things Being Observed

There are three categories to be considered:

Commodity: Commodities in this context mean final (usually consumer) goods and services.

Project: A “project” is an expenditure that encompasses multiple commodities. It can be either an investment, such as construction of a church or new factory, or a government expenditure, such as the financing of Medicare or a war. Also, within this category are such items as the size of a government budget deficit and the total assets or net worth of a company.

Compensation or Wealth: This is a flow of earnings or a stock of wealth. It can be the earnings of a specific type of labor, such as a star athlete or an ordinary plumber, or the (average) earnings of a broad group, such as teachers.

            Whatever the category, what is being observed must be expressible as the monetary amount of a unit, and it is the worth of that particular unit that is to be measured. The unit must be specified precisely, but the unit is arbitrary. Conventional units are often used (e.g., a gallon of gasoline or annual gas production, one loaf or 100 loaves of bread, an hour of unskilled labor or a professor’s annual salary). Also, an entire project or stock could be the unit (e.g., the U.S. Civil War, a government deficit, a person’s real-estate holdings). Anything may be assigned a “worth,” provided the “anything” is expressed in monetary terms (e.g., the price of a gallon of gasoline or a loaf of bread, the value of all bread production, the cost of a war).

 

The Measures

For a single point in time, there are three types of measures: an index of spending patterns, an index of output, and an index of income. The indexes used for each of these three measures are the expenditures of the average household, total output as measured by GDP, and two kinds of average wage and per-capita GDP, respectively.^[3] These do not comprise a complete list; there is good reason to think that other measures would be more appropriate in particular applications – as we will explain. An index of price will be added when we discuss comparisons over time and space. In each case, an item’s relative worth is obtained in comparison to a measure: the “formula” is to divide the value of the item by the appropriate index.

 

Household Expenditures: An often-asked question when deciding to buy something is, “Can we afford it?” Each person, each family approaches the market constrained by their budget. How much can be spent on entertainment has to be measured against what must be spent on food and housing. They are each part of the household’s total expenditures. Each purchase is measured against this total.

For the economy as a whole, an index called the “average household expenditure” (AHE) has been created.^[4] In the United States, average annual expenditures are measured by the Bureau of Labor Statistics’ Consumer Expenditure Survey.^[5] For 2017 there were 129,549,000 households in the country with an average size of two and half people with 1.3 earners. The mean income of these households before taxes was $74,664 and the measure of the AHE was $57,311. This is an average daily expenditure of $157. It is important to note that a hundred years ago, the average size of the household was three and a half people, so comparisons using this index do not reflect an individual’s relative value, but that of her family.

Sometimes specific bundles could be more appropriate. If one was writing a study of the spending by mine workers or the residents of a town named Springfield, then the average expenditures of those groups could be more informative than the AHE.

 

Output: The total production of the economy, customarily measured by GDP, is the most comprehensive, the most aggregated, measure to evaluate worth. The flow of GDP is usually reported as an annual measure, even when what is being reported is the quarterly change. However, the time period is arbitrary. The U.S. GDP of approximately $18.5 trillion per year corresponds to about $570 thousand per second. Again, more specific measures of output may be more relevant to a particular question. When talking about a government program, the size of the government budget or the size of the non-defense budget may be more appropriate.

 

Income: Any index of income can be used. The most frequently used measure of income is the wage rate, which can refer to a specific worker, a group of workers (for example, unskilled workers), or all workers. The time period for the wage rate (hour, day, week, month, or year) is arbitrary. For different comparators MeasuringWorth reports different measures of wages, such as average earnings, the unskilled wage rate, and the wage rate of production workers. A second measure is per-capita GDP, which can be interpreted as a person’s average share of GDP. Again, the time flow for GDP (year, quarter-year) is arbitrary.

 

We present here specific definitions for each of the combinations of one of the three measures applied to each of the three types of items. The nine are presented in Table 1. For each cell, the formula for a definition of a measure of worth is the ratio of the type of item to one of the three measures. We present how the three measures can be applied to the items as they are generally categorized.

 

Table 1 Measuring Worth: Point in Time
Item Measure	Commodity	Project	Compensation or Wealth
Household Expenditures	Relative Value in Consumption	Household Cost	Household Purchasing Power
Output	Economic Share	Economy Cost	Relative Output
Income	Labor (or Income) Value	Labor Cost	Relative Income (or Labor Earnings)

 

Household Expenditure

The first row of Table 1 involves calculations when the measure is a household expenditure.

 

Relative Value in Consumption – This measures the expenditure relative to the cost of the amount of goods and services such as food, shelter, clothing, etc., that an average household buy. This measure uses the daily average household expenditure (AHE), which is only available after 1900. Historically this bundle has become larger as households have bought more over time. For example, in 2017 the average nominal price of a one-pound loaf of bread was $1.33^[6]. Thus, we can say that the relative value of that bread was less than 1% (1.33/157) of the daily average household expenditure (AHE). In this case, the physical amount of the commodity is one loaf, but it could be greater, for example, the total number of loaves produced during a time period.

 

Household Cost – The cost of a project relative to the AHE. The project may pertain either to business/government, a person/household, or to a nonprofit institution. The construction of a church or a government project requires the use of resources that are then not available for current (say, consumption) expenditure.

 

Household Purchasing Power – This is measured as a household’s income or wealth relative to the AHE. For example, in 2016, the average wage in the United States according to the Social Security Administration was $46,640.^[7] This is only 82% of the AHE, so we are not surprised that with this purchasing power, the average household has more than one “bread” earner. On the other hand, the median average hourly wage of a neurosurgeon was $175, over nine and a half times the average hourly AHE. Given that the weekly AHE was $1,170, the neurosurgeon could cover that in about six hours of work (the cynic might say “and now have lots of time for golf.”) This can also be applied to stock variables. The reported wealth of Bill Gates is $93 billion, or a wealth that is worth about 1,630,000 of what the average household spends in a year.

 

Output

Turning to the second row of Table 1, we consider the alternatives when the relevant measure is output. As noted, GDP is the most common index used for the calculations involving this measure.

 

Economic Share – This is the worth of a commodity divided by GDP; it is its share of total output. This is helpful in measuring the relative value of aggregate consumption items such as all the cars made in a year. In 2017 there were over six million cars and trucks produced in the US. In the national income accounts, it is reported that the production of motor vehicles and parts was $498.2 billion out of a GDP of over $18 trillion. So the economic share of cars and trucks that year is 2.6%. For comparison, the $40 billion output of bread was a mere .22% of the output of the economy.

 

Economy Cost – This is measured as the cost of a large project or expenditure (e.g., large-scale investments, government deficits, or wars) as a percent of the output of the economy. This measure indicates the opportunity cost of the project as the share of the total output of the economy (GDP). It can be interpreted as the importance of the item to society as a whole. It is termed the Economy Cost (in contrast to the Household Cost which is the result of dividing by the AHE). For these larger output items, calculating the share of GDP is often the measure of choice because it focuses on the opportunity cost; the resources that produced the output in question in relation to the total output of the economy.

 

Relative Output – The ratio of income, compensation or wealth to GDP provides a sense of the share of the economy it represents, the amount of what we call the relative output it commands. Many believe that the rich have access to political favors that are denied to the average person. Their income and wealth relative to the output of the economy is a measure of their prestige.

 

Income

The final row of Table 1 is concerned with the measure of income. It should be noted that, since GDP is simultaneously a measure of output and income, the calculations here may be identical to those when output is the measure and GDP is used as the index of output.

 

Labor (or Income) Value – This measures the value of a commodity in relation to the average wage that a worker would need to use to buy the commodity. This measure uses one of the wage indexes (e.g., the wage rate or the earnings of unskilled labor). This measure gives the value of a loaf of bread in terms of the number of paid labor hours required to purchase it. In 2017 the average hourly wage of a food and beverage worker was $9.81 per hour.^[8] Thus for such a worker to purchase a $1.33 loaf of bread, it took (or had a labor value of) about eight minutes of labor.

Sometimes it is preferred to measure the value of a commodity in terms of an income measure (e.g., the average income of doctors or per-capita GDP). This measure is called the income value of the commodity. In 2017 and a new Chevy Cruze was $18,000 and the GDP per capita is $59,470. Thus, the income value of this car is about 30% of per-capita annual income. Similarly, the income value of a Cadillac Escalade is 126%.

 

Labor Cost – This is defined as a project’s cost measured relative to the average wage of the workers that might have been/be used to build the project. An example of a beneficial use of this definition is discussing the Erie Canal that was constructed mostly with unskilled labor. ^[9] The ratio of its cost to the unskilled wage is a good measure of its opportunity cost in terms of what else might have been built. Of course the cost of labor is only part (though often the largest) of the total cost. In some ways using the per-capita GDP mitigates some of this problem.

Relative Income (or Labor Earnings) – This measures an amount of income or wealth relative to the average income or wage of the average worker. If one’s wealth is used as the numerator, the ratio becomes Relative Wealth. It should be noted that whether an individual’s income or wealth is divided by an index of wages or salaries or divided by the annual GDP per-capita, the result provides an indication of their relative status in the economy.

 

Again in 2017, the food and beverage workers at $9.81 per hour earned a relatively low 40 percent of the average wage. These workers had a wage that not only involved low purchasing power (or low relative earnings) but also conveyed low economic status. In contrast, the neurosurgeons earned 1,200% of the average wage and, therefore, can belong to the best clubs and travel first class, an indication of their economic status.

 

Picking the Right Definition

In the context of Table 1, what is the appropriate cell to use when discussing the worth of a commodity? In most cases it is not one, but a combination of two or three! It is almost like the parable of the blind men and the elephant. Each is a correct answer, but they tell a different story.

Consider the sale of a particular commodity, a cutting board at a craft fair. The buyer is trying to decide the worth of it to give as a gift. She has a list of alternatives in mind, and the prices of these alternatives are a part of how she decides to buy or not. She also has a budget for all the gifts for which she is shopping. That budget is part of her total household expenditure and helps her determine the Relative Value in Consumption of the cutting board.

The seller of cutting boards has different thoughts about their relative worth. He may have been working as a carpenter building houses when he decided to try to supplement his income at craft fairs. His wage as a carpenter is an important opportunity cost. The income of plumbers might also be part of his calculation, but be less relevant as he may lack the immediate skills to switch easily to that career. In deciding what price he will ask for his cutting boards, he has an implicit index of the worth of his time, an index computed in a similar way that an average wage index would be computed. The seller is computing the Labor Value of his time constructing cutting boards.

In looking at projects all three terms can easily be used. If a historian is writing about the construction of a new church, there could be a discussion of the donations required of parishioners as a share of their annual expenditures or their household cost. The resources used to build the church also could be discussed, and a proxy for that could be the amount of labor they would have to hire or the labor cost. Another part of the story would be how important this church will be to the entire community. The cost of the church as a ratio of the community’s GDP or its economy cost would explain that.

Finally, almost any discussion of the wealth and income of the new super rich can use all three terms from the table. They have the household purchasing power to buy very large yachts; they donate large sums to political campaigns and have lawyers to help them reduce their taxes reflecting their relative output. And compared to (lowly) neurosurgeons their relative income would be many times greater.

 

Empirical Application -- 1931

As a case study, we report the worth of a number of subjects in one year, 1931. The year 1931 is chosen because it was a year of at least three memorable events, involving Babe Ruth, the Empire State Building, and Al Capone, respectively. Also, it is a year far enough in the past so that nearly everyone living today has no memory of what things cost then, therefore they cannot think in terms of what they remember.

In 1931, Babe Ruth, the indomitable baseball player and personality, was asked how he could justify his annual salary of $80,000, which was greater than that of President Herbert Hoover. The Babe made his famous reply: “I had a better year than he did.” This was also the year in which construction was completed on perhaps the most famous building of the twentieth century, the Empire State Building. That structure was completed in May 1931, taking only fourteen months to build; for forty years it was the tallest building in the world. The total cost of the building, including the land, was $40,948,900. Finally, the legendary gangster Al Capone was convicted in 1931 of tax evasion, of failing to pay taxes of $215,000 on income earned (albeit illegally) over the years 1925-1929.

It is of interest to expand the subjects to include the price of a common commodity and the wage for a particular occupation in the year 1931. A one-pound loaf of white bread, on average over several major cities, was priced at 7.7 cents, while an accountant earned an annual wage of $2,250. At the other extreme in magnitude, we take what is now called the defense budget of the U.S. government as the project expense. The total of outlays of the Departments of the Army and Navy for fiscal year 1931 was $839,910,000.

The worth of the 7.7¢ one-pound loaf of bread in 1931 is straightforward. The loaf had a relative value in consumption of 1.8 percent of the daily AHE, an income value of 4.5 percent of daily GDP per capita, and a labor value of nine minutes of work for a production worker to earn enough to pay the 7.7¢,

Turning to the accountant, his or her annual income sufficed to buy 1.43 household bundles—a decent household purchasing power for the period. The relative labor earnings of this occupation was over three and a half times the GDP per capita and 50% more than a full time, 60 hour a week production worker.

Of course, Babe Ruth’s household purchasing power was discernibly high, with his annual wage equivalent to 50 household bundles. The Babe’s relative labor earnings were correspondingly enviable: his wage constituted multiples 52 and 107 of the annual average wage of a production worker and the per-capita GDP. His relative output, measured as his income divided by GDP, was 25 times that of the accountant.

Capone’s unpaid taxes reflect a very large unreported income. It is reported that he said: “This is preposterous! You can't tax illegal money!” The fine of $215,000 alone constituted multiples of 146 and 345 the annual average wage of a production worker and the per-capita GDP respectively. Capone’s fine had 2.7 times the relative output of the Babe’s salary.

The household cost of the Empire State Building was 26,100 household bundles. The labor cost was 27,900, and 65,700 as multiples of the average wage of a production worker and the per-capita GDP. The economy cost of this project was 0.053 percent of GDP.

Finally, the defense outlays on the Departments of the Army and Navy for fiscal year 1931 had a household cost of 535,000 household bundles and its labor cost was 570,000 and 1,348,170 times the average wage of a production worker and the per-capita GDP. The defense share of GDP, its economy cost, was 1.08 percent, perhaps the most pertinent measure from the standpoint of society’s opportunity cost.

 

What is Something Worth at Another Time?

What is the worth today of an item in the past? There is a straightforward and literal answer to this question that is probably not what people expect. That is, find the price of the identical item in both periods and compare them. If the good does not exist today, then find something that is the analogue to that item and compare that. Take the example of a one-pound loaf of bread. As we have discussed above in 2017 the price of a one-pound loaf of white bread was $1.33 and in 1931 it was 7.7 cents. So, the “worth today” of a 7.7¢ loaf of bread from 1931 is $1.33. Q.E.D. That is an increase of 1,727%!

There are several problems with this comparison. First, there is no “1931 loaf of bread” in 2017. Yes, there are loaves of bread in 2017; but the 1931 loaf of bread may have been made from a quite different recipe with different ingredients. Even were the loaves to be identical, they may have played different roles in the overall diet – the consequences of which we do not know. And there were no Chicago deep-dish pizzas in 1931, and there is no Babe Ruth in 2017. There is a Kris Bryant in 2017, but he is not Babe Ruth.

Take the example of an ounce of gold that exists in both 1931 and 2017. Unlike most everything else, it is an exact analogy of itself; it exists in every year. In 1931 the price of gold was $20.67 an ounce, as fixed by the government. The average price of gold in 2017 averaged $1,257 an ounce. This is an increase of 6,082%!^[10] Another Q.E.D. But are these the number users want?

Visitors to the MeasuringWorth website often say they want to know what an item in the past is worth today. In nearly all cases, this is not the question they want answered. What they want is a current dollar amount associated with the worth of that past item they can compare to the values of all the known commodities, incomes, wealth, etc. today. They want an algorithm that transfers the value of that item to a “comparable” value today so they can compare it to “what they know.”^[11] The woman buying the cutting board may be thinking about a cutting board her mother gave her twenty years ago. She is wondering if the board she is buying today to give to her daughter has the same relative worth, of the one she received. Inflating by a price index is the usual, and often flawed, approach.

Consider how to measure the worth of an ounce of gold from year to year. If a historian writes, “In 1931, John went to Alaska and had a good month in that he found 5 ounces of gold (that is about $6,300 in today’s prices).” This is correct (5 times $1,257). But it is unlikely that is what a historian would write. If John had found $103.35 worth of gold in 1931 prices, it is likely she would have written (“that is about $1,660 in today’s prices”).^[12] She would have calculated that from the CPI Inflations Calculator on the BLS web site.^[13]

But the historian might have written that John could have exchanged the $103.35 for 80% of a month’s worth of the AHE (103.35/130.80) and that in 2017, 80% of the AHE would cost about $3,800 (a lot more than the $1,640.) And she could add that selling five ounces of gold today puts 50% more the table today that it did in 1931 (6,300/3,800).”

Prospecting for gold in 1931 was a good idea if John was out of work. But what is the relative value of prospecting measured by the wage he might have given up? What is the labor value of working in the gold fields? ^[14]   If he had been a production worker earning 51¢ an hour for 60 hours a week, in a month he would have earned $122. As an unskilled worker he might have made $90. So if John was unemployed or an unskilled worker and could prospect around five ounces of gold a month in the Alaskan gold fields, he made a smart move by heading north. If he had been a production worker, he should have stayed home. Today, with the price of gold fluctuating so much, it would be harder for John to decide. Assuming the monthly income of a production worker to be about $5,000, given the price of gold in 2012, John would only have needed to find three ounces of gold to replace potential production earnings. Today, he needs to find over four ounces per month to do the same.

This discussion about gold mined in 1931 has produced some meaningful comparisons in today’s terms. By determining the relative value in consumption and labor value of the five ounces of gold in that year, we can apply those relative values to today and report meaningful comparisons. Notice that these discussions contain many more things than “that is about $1,660 in today’s prices.” We have not used the term or concept “real price” or “real wage” to describe John’s expedition to Alaska.

 

The Additional Measure

Price Indexes: As has been noted, the price index most people choose is the Consumer Price Index, usually the variant for urban consumers. It is a fundamental principle of economics that changes in relative prices change the distribution of purchases. It is the application of the expenditure function that monetizes the process of maximizing a utility function subject to a budget constraint. So the “first order” measure of the relative worth of an item is a vector of all prices at the time of the purchase. (Those of close substitutes will be more relevant.)

 

Construction of the current real value of something bought in the past – the Consumer Price Index (CPI)

An item a household purchased in 2016 was associated with a vector of prices observed in 2016. If you could find a vector of those prices in 2017 such that the household bought the same item in 2017, you would have “the relative worth” of the fixed bundle from 2016. While it might appear appropriate to write Q.E.D., “case closed,” the question is answered, there are three problems with this solution.

First, there is no easy way to compare a vector of prices. How does one define the fixed market basket of goods? One solution to this problem is to create a single number that is a weighted index of the most relevant prices. If the item is something the average household buys, then a good index would be the price of the AHE.

Second, what if the item bought in 2016 no longer exists in 2017. The solution is to find a close substitute in 2017 for this item and use the price of the substitute in computing the weighted index.

Third, there are 2017 prices for other items (that would affect the purchase) that did not exist in 2016. The solution is to find a close substitute for the 2017 item and value the amount purchased of the substitute in 2016 at the 2017 prices of the substitute. If the item is something the average household buys, then a proxy for this process is to say that the utility of the item as part of the bundle that was bought in 2016 would be the same as the utility derived from its consumption in 2017 when and if it exists. Appendix A discusses how the CPI has been constructed from 1774 to the present.

 

(Another way of) Construction of the past real value of something bought in the present – the GDP deflator.

What if the question is not comparing the value of the same item between one year and another? What if we just wanted to know the value of what you spent today in an earlier year’s prices? Then we do not have to worry about items from the past that no longer exist today, nor how much of each item was purchased, but we do have the second problem mentioned above in reverse. That is, there is no price in the earlier year for an item bought today. That happens more and more the farther in the past one goes. There are no prices for smart phones in 1931. The solution is to find the price in the past of a substitute for these items. It is important to note that the GDP deflator is not measuring a fixed bundle of items.^[15]

 

Three more Definitions of Relative Worth

The nine definitions presented in Table 1 were for a point in time. We used them to discuss the relative worth of different items using three measures. These definitions are equally useful for discussing relative worth over time as we demonstrated in the discussion of the gold prospector.

Using the Average Household Expenditure as the measure, we found that the daily relative value in consumption of a one-pound of bread in 2017 was $1.33 divided by $157 or 1/118^th the AHE. The daily relative value in consumption of a one-pound of bread in 1931 was 7.7¢ divided by $4.30 or 1/56^th the AHE. The relative value of bread was more expensive then. But another way to look at this would be to ask, what is 1/56^th of the daily AHE in 2017? The answer is that a 7.7¢ loaf of bread in 1931 has a relative value in consumption of $2.80 in 2017. Notice this computation does not involve the price of bread in 2017, nor does it even require that bread exists in the current year. This is the answer found on the MeasuringWorth comparator for the relative worth of the US dollar.

The other definitions work the same way. Using the income measure to discuss the $2,250 accountant’s salary in 1931, we find that the relative 2017 household purchasing power of his salary was $84,700, and his relative labor earnings of $109,000 or $142,000, and his 2017 relative output was over half a million dollars. Each of these is computed by multiplying the ratio of the observation of the measure in 2017 to the observation of the measure in 1931 times the salary of $2,250.

Table 2 adds the additional measure of a price index, and there are three real definitions in the final row.

 

Table 2 Measuring Worth: Another Time
Item Measure	Commodity	Project	Compensation or Wealth
Price Index	Real Price	Real Cost	Real Wage (or Wealth)
Household Expenditures	Relative Value in Consumption	Household Cost	Household Purchasing Power
Output	Economic Share	Economy Cost	Relative Output
Income	Labor (or Income) Value	Labor Cost	Relative Income (or Labor Earnings)

 

Real Price – Real Price is measured as value of a commodity relative to the value of a (fixed over time) bundle of goods and services such as food, shelter, clothing, etc. (e.g., the CPI), that an average household would buy. In theory the size of this bundle does not change over time, but in practice adjustments are made to its composition. Using the CPI, the real cost of a commodity in 2017 in 2000-year prices would be its current price times (172.2/245.12) or 70.3% of the current price. The real price of a commodity in 2000 measured in 2017 prices would be a multiple of the inverse (245.12/172.2) or 142.3%. If one preferred to use the GDP deflator, the values would be 72.2% and 138.5%.

Returning to the story about John and his 5 ounces of gold in 1931, what would the real value of $1,660 add to the story? What does it represent? The interpretation is that when John sold his five ounces of gold and received $206.70, that he could go to the store and buy a particular bundle of 1931 household goods including food, clothing, housing and other goods, and services such as a ride on a streetcar (though there might not been any around in Alaska.) The $1,660 is the price of “that bundle” today. It is not the same bundle as in 1931; it is an analogue of that bundle that includes other forms of transportation and the use of a smart phone.

 

Real Cost – This is the cost of a project measured by comparing its cost to an index of prices for all output in the economy (e.g., the GDP Deflator). Sometimes using the CPI makes sense. If the parishioners are wondering how much those donations of $1,000 each made to build a new church 16 years ago “are worth today,” using the CPI, they would conclude it was $1,420.^[16] For larger projects, it usually makes more sense to use the GDP deflator.

 

Real Wage (or Real Wealth) – The real wage measures the purchasing power of an income (be that an hourly wage, yearly salary, or an end of year bonus) by its relative ability to buy a (fixed over time) bundle of goods and services such as food, shelter, clothing, etc. (e.g., the CPI). In most cases, the real wage is constructed using the CPI index. The idea is that recipient of this compensation is going to spend it on items in the household bundle, so the real wage has now been converted the purchasing power of a fixed bundle of consumer goods.

The story of the real wealth is measured the same way, but we are talking about comparing a stock to a flow. A person can have the same nominal wealth year after year, but his or her real wealth will change. It should be noted that when these compensation or wealth amounts are substantially different than the AHE, the computation provides less meaningful information. When comparing the wealth of Andrew Carnegie and the wealth of Bill Gates, the relative amount the AHE each could buy is not an interesting question.

 

Selection of Measure

In general—and contrary to the almost-universal application of the CPI—there is no definitive answer to the question of worth over time. The questioner has first to decide on the context. Nevertheless, some guidance can be given. Most of the discussion for the point-of-time (single-period) schema is applicable when comparing over time and in many cases those first nine definitions are preferable.

The real price using a price ratio involves only pure-inflation; the bundle underlying the measure is unchanged from the base period. In contrast, relative value in consumption using the AHE measures the share the item is of a period-specific household bundle in period 1 to the share of what that bundle would cost in period 2. This latter answer incorporates both the change in price and the change in the size of the bundle itself. In fact, that property generally causes the relative value in consumption to be preferred to the real price concept, as the difference found only from pure inflation cause substantial misimpressions over time, as will be shown below. While one might consider that the use of the GDP deflator to compute the real price might alleviate this problem, in most cases it does not. Changes in the GDP deflator reflect changes in all prices (both consumer and producer goods) and total output. There is no particular item being measured. When the item discussed is a commodity, a price index of both consumer and producer goods and services would be inappropriate.

The GDP deflator is a much better measure to compute the real cost, particularly when the project is large, such as the construction of a highway system. The real cost could be compared to similar measures that would be appropriate for the particular item. For example, the BEA publishes 26 GDP deflators for all the related components of the economy.^[17] In many cases, defining the real cost using a specific deflator will tell a more interesting story.

As discussed above, using Real Wage (or Real Wealth) also has problems with the issue of what the price index measures. The intent of computing a real wage is to suggest each dollar of compensation in both periods has the same purchasing power of groceries, housing, entertainment, etc. This is done by dividing each wage of a particular year by the CPI of that year. The greater the difference between the two years, the less comparable the content of the bundle and the less the real wage has the “same” denominator.

In certain situations, the appropriate measure of worth is clear. If the question is whether “Andrew Carnegie in 1900” was wealthier than “Bill Gates in 2017,” then neither the CPI nor a wage-rate index provides the appropriate comparison formula. Rather, Carnegie’s wealth should be inflated by the ratio of GDP in the two years. “Relative output” as represented by share of GDP—not relative earnings or status—is the criterion. In most contexts, the worth across time of large-scale, public-good projects (such as war or space exploration) is again obtained most meaningfully by the GDP ratio, not by the CPI or GDP deflator.

The important point of all this discussion is that in most cases using multiple definitions of worth is the best. They all describe the elephant.

 

Empirical Application – 1931 measured in 2017 prices

We now consider the relative worth of the 1931 subjects eight-six years later in 2017. As we have explained the technique is straightforward. We find the worth in 1931 using one of the nine definitions in table 1. These definitions are based on three types of measures. We then take the observation of the value of the item in 1931 as a share of the index number for that measured in 1931. That share is then multiplied times the observation of the measure in 2017. Now we can also use a price index for the three additional definitions.

That loaf of bread in 1931 had a relative value in consumption of 1.8 percent of the daily AHE, and an income value of 4.5 percent of daily GDP per capita. The labor value for a production worker was eight minutes of work. Applying those ratios to the 2017 values of the AHE, GDP and production worker’s wage and we get that the relative value of that 1931 loaf of has a real value of $2.92, an income value of $7.33 and eight minutes of a production worker’s wage would earn $4.31 or labor value. Of course, we now can also compute the real price and that would be $1.24.

Applying this technique to the accountant’s $2,250 salary in 1931, we see that this money had a relative 2017 household purchasing power of $84,700 and relative labor earnings between $109,000 and $142,000 and relative income of $215,000. Using the CPI to inflate this wage gives a real wage of $36,200. By just looking at this relative real wage (that is 75% the average wage of all workers and a little over half the median wage of $69,350 that accountants earn today^[18]), you would conclude that accountants were very poorly compensated. On the other hand, the relative earnings look as if accountants were extremely well compensated.

Babe Ruth’s 1931 income has a 2017 real wage of $1,250,000, which does not sound very large when one considers the average salary for a major league player in 2017 was $4 million! Even when we look at the Babe’s relative income at $7.6 million, they do not compare with the $33 million paid to Clayton Kershaw in 2017.

The real cost of Capone’s fine is $3.5 million. The 2017 measure of the real earnings lost by the fine is $20.5 million. This seems quite small compared to the quarter of a billion-dollar fines that have been passed out these days.^[19]

The 2017 real cost of the Empire State Building is $543 million (using the GDP deflator). The household cost is $1.54 billion, while the labor cost is $1.98 billion or $2.6 billion (using the unskilled and the production worker wage). The economy cost is an impressive $10.3 billion as measured by share of GDP. This can put in perspective the announcement that 2 World Trade Center will likely cost $4 billion.

Finally, the worth in 2017 of the 1931 defense spending also, of course, has the same fourteen-fold range. The real cost (using the GDP deflator) is $11.1 billion, whereas the AHE generates a worth of $31.6 billion household cost. The labor cost is $40 billion or $53 billion (using the unskilled and the production worker wage). The defense share of output is $210 billion. As a comparison, the defense budget for fiscal year 2017 was $583 billion. Of course, our methodology would emphasize that the subjects are not “the same” defense.

 

 

Conclusions

This paper discusses the many ways to the compute the relative worth of an item and demonstrates that any item with an associated monetary amount can have its worth measured in many ways -- both at a moment in time and over time. The different definitions of relative worth presented show how important context is. The paper shows that statements of worth are meaningful only when the contexts are specified and that the almost uniform use of the CPI (particularly by itself) to measure worth over time is often misleading. Although there may be an implicit or explicit assumption that all these definitions will tell about the same story as we talk about the past, that by using one we are implying the others, this paper has shown how wrong that is. Table 3 shows how much these measures differ, and how much more they differ the farther one goes back in time.

 

 

The ideas discussed in this paper were included in a submission to the Quarterly Journal of Economics in 2005. That paper was more technical and contained a formal model, but the theme was the same. The article was rejected based on the following referee’s comments.

 

…the CPI answers a specific economic question of great relevance. It estimates a first-order approximation to the expenditure function, and therefore provides an approximate measure of the amount of compensation required to allow an individual to purchase her consumption bundle at time t, but at time t + 1 prices.

Using prices to compare worth at a point in time and price indices to compare it over time is an imperfect approach, to be sure. Sometimes dollar prices are not readily available and must be imputed or calculated from a model as shadow prices. And there are many well-known flaws with index numbers. But these approaches are well-defined attempts to answer specific economic questions of measurement; the measures provided here are not.

 

Sometimes imperfect and flawed should over rule well-defined approaches.

Therefore, to conclude, here is a list of suggestions for authors to use in their work and for journal editors to request of their authors. It is not inclusive, and more discussion is warranted.

1.     Any statement of real price or real wage must define the index being used.

2.     The term “in 2016 dollars” or “in today’s dollars” should not be allowed by itself. At the minimum there should be a footnote declaring what index is being used to make the conversion.

3.     The use of the CPI to generate the term “in 2016 dollars” or “in today’s dollars” should not be allowed for comparisons where changes in the content of the AHE would impact the comparison.^[22] Usually relative value in consumption and income value are better measures.

4.     For the purpose of putting a value in current perspective, as a general rule, the CPI should not be used earlier than the time that most readers have a memory of what was in the consumer basket.

5.     The terms “real prices” or “in today’s dollars” should not be used for computations involving the CPI unless they apply to a consumer good or service.

6.     In time series data, the CPI should not be used to deflate a price or wage series without a statement of why it is better than other measures.^[23]

7.     When comparing two or more series in the past, ask the question does deflating them by the cost of a fixed consumer bundle (the CPI) add information? This is probably not a good idea, particularly if they are dissimilar items.^[24]

8.     If a model is being tested using “real derived variables,” ask the question is there any reason it could not be tested using nominal ones instead?

Appendix B shows examples from the press and publications that could have been improved by using these rules.

 

Appendix A

The History of the Consumer Price Index (CPI)

 

MeasuringWorth publishes an annual CPI series from 1774 to the present. Before 1914, the series is based on various contemporary studies made in the 19^th century and on the work of many 20^th century economic historians that was put together in the classic work by Peter Solar and Paul David in their study “A Bicentenary Contribution to the History of the Cost of Living in America.” ^[25] The numbers reported since 1914 have been published by the Bureau of Labor Statistics.

The earliest numbers come from fitting a regression to Philadelphia wholesale prices. Then for the years from 1800 to 1851, six benchmark years of retail prices and budget collected by Dorothy Brady and the interpolated by an annual series of what Vermont farmers paid.

During the latter half of the 19th century, various economic events prompted Congress to ask the Bureau of Labor (later to be renamed the Bureau of Labor Statistics) to collect information on the “cost of living.” These data were needed to discuss such issues as tariffs and labor unrest. At the turn of the century “the Bureau endeavored to conduct a comprehensive study of the condition of working families throughout the country. A survey of family expenditures from 1901 to 1903 was the first step in constructing “a comprehensive index of retail prices.”^[26] More studies were made over the next two decades and then “Using a weighting structure based on the 1917–1919 expenditure survey, in 1919 the Bureau began semiannual publication of a retail price index. With the reference base period set to 1913 = 100, values of the index were estimated back to 1913 with the use of wholesale price movements.” (It did not get its current name until 1945 when it became the “Consumer’s Price Index for Moderate Income Families in Large Cities.”)

These studies were used extensively by the government for policy purposes such as to standardize and stabilize wage rates during U.S. involvement in World War I. A specific example of the use of the index during the depression was the passage by Congress of the Economy Act of 1933 requiring a 15-percent reduction in federal salaries on the basis of a more-than-20-percent decrease in the BLS cost-of-living index.

From the beginning, the indexes were met with much criticism for the lack of inclusiveness in the number of cities used and the diversity of the families surveyed, the slowness of updating the composition of the fixed basket of goods and services, and whether the technique of using a fixed basket was the best measure of the ideal “cost-of-living” index.

During the last 85 years, many commissions and studies have critiqued the index. In the 1940s there were the Mills and Mitchell Committees then, the Stigler Committee in 1960, and the Boskin Commission of 1995. Each made recommendations; some accepted, and others not.

The conflict during WWII between organized labor and the Bureau demonstrates the main issue when “American Federation of Labor (AFL) Representative George Meany stated, ‘If the index is a retail price index and not actually a cost-of-living index, we have no particular interest in what the index has done in the past…. My attitude is…let’s go into partnership and see what we can do together—this committee and your department—to make the index do the thing that it has not done.’ Commissioner Hinrichs insisted that, by definition, cost-of-living indexes were constant-good, retail price indexes, and as the Mills Committee report explained, this type of index was limited in its ability to fully capture changes in all factors that affect an individual’s well-being.” The Mitchell Committee also agreed with the Bureau’s position that many were confusing the additional expense of attaining a higher standard of living for an increase in the cost of a fixed standard of living.

In 1960, the Stigler Committee was formed to address among other issues, the question if the CPI overestimated inflation. It the opening statement was critical when they say:

“But in the presence of the introduction of new products, and changes in product quality, consumer tastes, and relative prices, it is no longer true that the rigidly fixed market basket approach yields a realistic measure of how consumers are affected by prices.”

The committee recommended changing the CPI to a “constant-utility” index, but in the end a 1964 report stated that, “The revised CPI, continues to be what it has always been—a measure of price change, and of price change only, in items purchased by urban wage and clerical workers for their own consumption.”

In the 1970s the BLS wanted to replace the CPI based only on the surveys of urban wage earners and clerical workers (the CPI-W) with a broader CPI-U population. Some users resisted the change, so from 1978 both indexes have been published. Today, the CPI-W is used to calculate Social Security cost-of-living adjustments, most other cost of living adjustments, such as the indexation of federal income tax brackets, uses the CPI-U.

In 1985, complaints about biases of the CPI were the reason for the creation of the Boskin Committee. Their final report stated because of two levels of substitution, new product or quality change, and new outlets, the CPI over-indexed by .80 to 1.60 percent. While some of its recommendations were accepted, and starting in 2002, the BLS began publishing the Chained Consumer Price Index for All Urban Consumers (C-CPI-U), that series is not used to make adjustments to Social Security or any other federal program and the CPI-U is still the series that is reported on the 15^th of the month.

While the CPI may be the best measure of inflation (and the only one we have before 1909), it is appropriate that the content of the market basket used to construct the CPI changes over time to reflect the changes in household spending patterns. However, when using the CPI to inflate a price from the past, these changes create an incomparable bundle of which most users are unaware.   In particular, in the constructing of the CPI for the antebellum period, purchases of food made up about 40% of the bundle and clothing 22%. 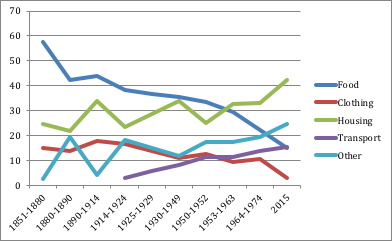As recently as the 1950s, those same items made up 33% and 13% while in 2017, those same items made up 15% and 3%.

 

 

David, Paul A., and Solar, Peter. (1977). “A Bicentenary Contribution to the History of the Cost of Living in America.” In Paul Uselding, ed., Research in Economic History, vol. 2, pp. 1-80. Greenwich, CT: JAI

Bureau of Labor Statistics (2015). The first hundred years of the Consumer Price Index: a methodological and political history, Monthly Labor Review. http://www.bls.gov/opub/mlr/2016/article/one-hundred-years-of-current-employment-statistics-busting-ces-myths.htm

Officer, Lawrence (2019 What Was the Consumer Price Index Then? A Data Study. found on Lawrence H. Officer and Samuel H. Williamson, "The Annual Consumer Price Index for the United States, 1774 to the Present," MeasuringWorth, 2019.

URL: http://www.measuringworth.com/uscpi/

 

 

Appendix B

 

Two Examples from the New York Times

In the New York Times on 12 February 2016 there was an article titled “George Washington, the Whiskey Baron of Mount Vernon” by Michael Beschloss. There were statements in the text that were intended to give the readers a sense of how much Washington’s expenses and income were.

When a nephew asked the ex-president for a loan of $1,000 (about $18,000 today), Washington gave in but admonished him, ‘You are under the same mistake that many others are in supposing that I have money always at command.’

What would that $1,000 the nephew received buy? In 1800, an axes cost $.50 each; a gin, $1.11 a gallon; sugar, $12.94 a hundred weight; and lumber, $28 a thousand feet. So with $1,000, the nephew could have bought 2,000 axes, 900 gallons of gin, 7,800 pounds of sugar, or 36,000 feet of lumber. At today’s prices, $18,000 can buy 500 axes, 350 gallons of gin, 28,000 pounds of sugar, or 60,000 feet of lumber. So in terms of commodities available both then and now, the “about $18,000 today” is not a bad guess.

But we can doubt that in the mind of the average reader when they see this amount, they are thinking about the axes or lumber they have just purchased. They might think that $18,000 might buy a decent used car or pay the tuition for a year at a junior college.

In 1800, with $1,000 that nephew could have bought 500 acres at the price of $2 an acre most anywhere as that was the minimum price set in the Land Ordinance of 1796. Unimproved land most places today, would value that at half a million or more. He possibly could have bought a herd of 50 to 100 cattle, which would be worth about $1,000 a head today. Or he could have bought three slaves or more that have a labor or income value of over $150,000 at current prices.[27] The idea that this loan should be thought of as about $18,000 today misrepresents its magnitude.

 

Here are the results from the MeasuringWorth US comparator he could have used:

The relative price in 2015 of $1,000.00 from 1800 is:

$19,500.00 using the Consumer Price Index

$18,300.00 using the GDP deflator

The relative wage or income in 2015 of $1,000.00 from 1800 is:

$310,000.00 using the unskilled wage

$764,000.00 using the Production Worker Compensation

$619,000.00 using the nominal GDP per capita

The relative output in 2015 of $1,000.00 from 1800 is:

$37,600,000.00 using the relative share of GDP

 

Another article from the New York Times on 16 April 2016, there was an article titled “272 Slaves Were Sold to Save Georgetown. What Does It Owe Their Descendants?” The article does not say how much they were sold for, but the author (or the Times editor) attempts to put the sale in current perspective with these two sentences:

And the 1838 sale — worth about $3.3 million in today’s dollars — was organized by two of Georgetown’s early presidents, both Jesuit priests. Some of that money helped to pay off the debts of the struggling college.

The 2015 budget of Georgetown is $1,147.9 million. Thus, the story implies that Georgetown sold these slaves to cover one day of its expenses (by using a purchase power calculator.)

Is this what the author wanted to say? 3.3 million divided by 272 is about $12,000. Perhaps it is an unintended consequence of the article to say the average value of slaves in 1838 is $12,000 in today’s prices. That is not much and that was a year when slave prices had reached a peak. The article “Measuring Slavery in 2011 Dollars” puts the labor income value of the average slave at ten times that amount in 1838.^[28]

Another source puts the sale at the contemporary price they received for the slave was $115,000. This would mean for this sale, the labor cost was as much $65 million and the economy cost $1.3 billion. It would have added a considerable amount of information if the author had reported what the annual budget of Georgetown was in 1838.

 

Here are the results from the MeasuringWorth US comparator the author could have used:

In 2015, the relative price worth of $115,000.00 from 1838 is:

$3,020,000.00 using the Consumer Price Index

$2,620,000.00 using the GDP deflator

In 2015, the relative wage or income worth of $115,000.00 from 1838 is:

$27,500,000.00 using the unskilled wage

$60,600,000.00 using the Production Worker Compensation

$65,500,000.00 using the nominal GDP per capita

In 2015, the relative output worth of $115,000.00 from 1838 is:

$1,300,000,000.00 using the relative share of GDP

 

Example from the Monthly Labor Review

There is an excellent history of the CPI in the Monthly Labor Review in 2015.^[29] It is not surprising that the article uses the concept “in current dollars” to describe the cost of creating the index when it was first started.

It states that “Commissioner Meeker worked quickly and earnestly to secure funding to complete the study and ultimately received $75,000 (approximately $1.35 million in 2012 dollars) from President Wilson.” This was in 1917 and the $1.35 million quoted here comes from using the BLS CPI Inflation Calculator.^[30]

Is that the story we want to know? In 1917, non-defense spending by the Federal Government was $700 million ($2,308 million minus $1,608 million). The $75,000 received to do this study was .011% of $700 million.

In 2012, the non-defense spending was $2,687 billion ($3,537 billion minus $850 billion) and .011% of this amount is $288 million. If we exclude off budget expenditures from the 2012 expenditures, then non-defense spending is $2,179 and .011% of this amount is $240 million.

So to understand the 2012 relative value of the $75,000 that Commissioner Meeker secured, the choice is:

1.     $1.35 million measured by what the average urban household spends (which in 1917 was over 40% was food.)

2.     $7.14 million measured by the compensation of the average production worker representing the cost to hire the people to do the work.

3.     Over $200 million that represents the share of the federal budget that was allocated to this project.

Later in the article they use the concept of “in current dollars” to explain the magnitude a change in the CPI will have on indexed Federal Expenditures.

By 1981, “almost a third of federal expenditure [was] directly linked to the CPI or related price measures, and over half of the federal budget [was] affected if indirectly indexed expenditures [were] added.” Small movements in the CPI could dramatically affect government outlays; for example, a 1-percent increase would “automatically trigger nearly $2 billion of additional federal expenditures, at 1981 program levels [approximately $5 billion in 2012 dollars].”

What are the authors trying to say is the meaning of this $5 billion? The CPI had increased from 90 to 230 between 1981 and 2012 or a little over 2.5 times. On the other hand, Federal Expenditures, nominal GDP and social security payments had all increased over five times during that period. So, if this number was inflated by the size of federal expenditures, it is probable that a 1-percent increase in the CPI would “automatically trigger over $10 billion of additional federal expenditures, at 2012 program levels.”

But the amount Federal Expenditures in 2012 would increase from a 1-percent increase in the CPI could be even more than this, since more programs might be indexed by then. It is not clear what the authors are trying to say since it appears that this quote is from a 1981 article about indexing with the CPI. So the statement “approximately $5 billion in 2012 dollars” adds confusion. It would have been better to index the $2 billion to the share of GDP or share of the federal budget.

 

Examples from Journals

Here are two examples where a version of the expression “in today’s prices” was used.

Any time an article uses the term “real cost” or real wage” there is an implicit or explicit denominator associated with the term. Some articles do better than others.

In the article titled “Do Patent Pools Encourage Innovation? Evidence from the Nineteenth-Century Sewing Machine Industry,” The Journal of Economic History, Vol. 70, No. 4 (December 2010), pp. 898-920: There is the following: “The pool agreement …. was to be maintained above $10,000, approximately a quarter million 2009 dollars … Then there is a footnote: “Using the Consumer Price Index, $10,000 in 1856 was worth $261,000 in 2009. Other indicators place the value of the litigation fund between $198,000 and $35,600,000 (Williamson, Six Ways).

It is nice that the authors know that there are other indicators, but what do the authors want readers to do with this information. Why didn’t they pick one or more and explain why they chose it? Of course, using the CPI violates rule one, but even if this was a study of pool agreements today, why would anyone want to know the value of the agreements measured in a multiple of consumer bundles? It would be more interesting to measure this against the output of the sewing machine industry. If they did not know that, then would the GDP be a better proxy than the AHE? It would be worth thinking about.

 

In the article titled “Flip the Switch: The Impact of the Rural Electrification Administration 1935–1940,” The Journal of Economic History, Vol. 75, No. 4 (December 2015), pp. 1161-1195: there is this sentence: “In its first five years of operation from 1935 to 1939, the REA provided more than $227 million in loans ($3.6 billion in 2010 dollars) primarily to newly incorporated cooperative utilities, to survey areas, lay distribution lines, and wire homes.” The GDP in 1937 was $93 billion, all government expenditures $13.1 billion, and non-defense federal expenditures $3.8 billion. $227 million is .024%, 1.73% and 5.97% of these three measures of output.

The GDP in 2010 was $14.96 trillion, government expenditures $3.174 trillion and the non-defense part $833 billion. So by applying these output shares to these amounts, in today’s terms the $227 million in loans would be a $36.5 billion in relation to the present GDP, its economy cost. It would be a $55 billion in relation to all government expenditure today, and a $49.8 billion in relation to the non-defense part of federal expenditures. These amounts are ten or more times the “real cost” reported. These numbers are the economy cost of the loans, not a bad application of the real cost that would have added to the story.

 

In the article “Biological Innovation and Productivity Growth in the Antebellum Cotton Economy,” The Journal of Economic History, Vol. 68, No. 4, (December 2008), pp. 1123-1171, there is the statement: “From 1800 to 1860, the quantity of cotton produced increased by 6.6 percent per annum as the real price of cotton fell by 0.5 percent per annum. Over a slightly shorter period beginning in 1804, the U.S. slave population rose by 2.4 percent per year while the real price of prime-age male slaves rose by 1.9 percent per year.” In other words, an important part of the story is that slaves were a major input in the production of cotton, yet their real prices were soaring at a time when real cotton prices were declining.

The authors explain they are deflating slave and cotton prices by the series Cc113 from the Historical Statistics. This series is a wholesale price index. So, what they are saying is the price of cotton relative to other wholesale items is going down and the price of slaves relative to the same wholesale items was going up.

What does the “conversion to real price” add to the story that the cost of a slave per bale of cotton is rising? They could have deflated the slave price by the unskilled wage and compared the labor value of slaves to the real price of cotton. That would have been a different story.

 

In the article “On the divergence between fuel and service prices: The importance of technological change and diffusion in an American frontier economy,” Explorations in Economic History, Vol. 60 (April 2016), pp. 93-111, the introduction does it right. It starts with an explanation of why not to use “conventional price indexes” and what will be used instead.

“In their most basic form, price indices are weighted- averages used to summarize price changes and to convert nominal to real values. Such indices assume that, for a given good, the consumption weights are comparable across time; i.e. the same good of the same quality is being consumed. However, consumption is more appropriately defined in terms of services. This distinction is crucial for energy fuels. These are inputs used in the production of services upon which welfare ultimately depends. As technology that transforms inputs to services matures, fuel prices and service prices may change to different degrees and in different directions. In such contexts, conventional price indices are likely biased.”